Welcome to siqili's Blog!
要多想-
Review of Causal model in RL
- Causal Confusion in Imitation Learning
- Causal Reasoning from Meta-reinforcement Learning
- Causal Induction from visual observations for goal directed task
- RECURRENT INDEPENDENT MECHANISMS
- Inductive Biases for Deep Learning of Higher-Level Cognition
Causal Confusion in Imitation Learning
本文强调/引入了一个概念:知道得越多,可能表现得越差( access to more information can yield worse performance)。直观地说,数据集分布的偏移(distributional shift)可能会导致模型学到动作(Action)和一些无关的噪音之间的联系,而无法学到其和真正的因子(causal parent)之间的联系。也就是说,当我们想要得到一个对分布偏移现象表现稳定的策略时,我们做决策时必须仅仅依赖那些真正的因子。
为了更好地说明这个现象,该文设计了一个符号附加在观测图像上的特殊环境,实验表明此时需要更多地样本才能学到在原先环境一样的性能。
定义: 分布偏移可以定义为对一个图中某些点($X$)的干预(intervention),记受影响的点为$A$,那么我们关注的结果就是$p(A|do(X))$.
为了解决因果误识(causal misspecification)的问题,这篇文章提出: (1) 为每一种可能的因果结构$G$(这里只考虑观测是动作的因子,故有$2^n$种可能,$n$是观测的维度)都学一套策略:$\pi_G(X)=f_\phi(X,G)$,优化目标就是最小化: \(\mathbb{E}_G [\ell (f_\phi(X_i\odot G,G),A_i)]\)
(2) 计算似然概率 $\mathcal{L}(G)$。此时分两种情况:
- 可以询问专家:

- 不能询问专家:

笔者的疑问:
(1) 如何能用线性回归学$w$? $w$ 是一个$2^n$维向量还是$n$维向量?
(2) 为什么 $f_\phi$ 是在$\mathbb{E}_G$下学的,而不是一个给定的$G$?
Causal Reasoning from Meta-reinforcement Learning
本文探索了用元强化学习辅助因果推理的可能性。
因果推理有两种:因果效用推理(causal-effect reasoning)和反事实推理(counterfactual reasoning)。前者指在去掉混淆因子的干扰下,正确地计算出因子对结果的效用/影响力;后者指在当前的因果结构和已发生的事实下,估计做另一种决策后会发生的事实。这两种推理都要求智能体能做到一些额外的事情,比如能够干预(即强行修改观测中的某些值,并得到环境的反馈,类似于RL中常说的reset)。因此,本文还设计了三种数据场景来实现因果推理:
- 观测场景:智能体只能被动地拿到数据。在该场景下,智能体可以做相关性推理和给定因果结构下(即已知因果结构)的因果推理。
- 干预场景:智能体可以对数据做干预并得到干预后的结果。此时可以做因果效用推理。
- 反事实场景:智能体可以通过执行干预来学到正确的因果结构。此时可以利用观察到的已发生事实和因果结构来推断出隐藏变量(可能是随机变量)的取值,并基于这些值正确推断出反事实的结果。
PS:本文是在用强化学习给因果推断问题建模,之后有时间再细读。
Causal Induction from visual observations for goal directed task
本文认为虽然数据驱动的方法有很多成功实例,但缺少正确的因果建模是目前泛化问题的主要诱因。本文中,作者提出了一个因果归纳/发现(causal induction)加因果推断(causal inference)的方案来使得智能体可以做因果推理(causal reasoning)。

本文考虑的是一个基于目标(goal)的RL环境,其中奖励函数是$r:\mathcal{S}\times \mathcal{A}\times \mathcal{G}\to \mathbb{R}$,策略也是基于目标的:$\pi_G:\mathcal{S}\times\mathcal{G}\to\mathcal{A}$。该文不仅希望学到的策略可以在不同的目标(G)之间泛化,还希望可以在不同的MDP(转移函数)之间泛化。 但是,本文有一个比较强的假设,就是可以拿到高维图像输入的低维表征-因果宏变量(causal macro-variable),其中包括了cause和effect的宏变量(例如图像包含了电灯开关和照明度,智能体可以直接得到反应开关的状态/cause和照明度状态/effect的变量)。
在第一步的因果归纳中,本文采用了一种迭代更新因果关系的方式。从无任何因果关系的初始结构开始,不断网上添加新学到的因果关系(类似往一个图上加边)。对每一个观测$o_t$,通过一个编码函数映射成$s_t$,再把这个表征的残差$R=s_{t+1}-s_t$和动作$a_t$拼在一起:$(s_{t+1}-s_t,a_t)$,再讲这个输入一个解码器(edge decoder),生成一个边$\Delta \hat{C}$,从而得到新的因果关系$\hat{C}_{t+1}=\Delta\hat{C}+\hat{C}_t$。其中生成$\Delta \hat{C}$时,是先生成一个注意力向量$\alpha$和一个边权向量$\Delta e$,再内积得到结果(此处对这两个量解释过少,让人难以理解)。从数据中收集完所有因果关系,形成了$\hat{C}_H$后,再把$\hat{C}_H$输入另一个网络生成最终的因果结构。
\[\hat{C}_{t+1}=(\alpha^T\Delta e)+\hat{C}_t, \alpha=\phi(R,a)\]
在第二步的策略学习阶段中,先基于当前状态和目标状态生成一个对效用上的概率分布$\alpha$(即为了达到目标,各个效用/effects的似然概率),再基于效用分布和因果关系的内积得到$e$(即为了达到目标,各个动作的似然概率),再将$e$和$(s,g)$的表征一起映射到动作空间。


这篇文章主要的不足在于并未真正完成声称的“在图像级数据上实现因果归纳和因果推断”,而是借助了宏变量来完成,即在宏变量基础上学习网络结构,而无需把宏变量给学出来。另一方面,值得借鉴的是它在因果归纳中采用了迭代更新的方式,而不是一步到位的因果发现,这或许也是一种可行的思路。
RECURRENT INDEPENDENT MECHANISMS
本文认为(稀疏的)模块化的网络结构可以让网络获得更好的泛化性能和稳定性。这里的模块化具体是指把神经网络分解成一个个子网络,让输入按指定的(但对不同的输入可能并不固定)顺序通过这些子网络并输出结果。这个想法来自于“模块化的结构下,改动其中一个模块的参数时,可能不会改变其他模块的参数,从而带来一定的稳健性”(换句话说,如果我们在训练中可以只改变一个模块的参数就达到好的训练效果,那么其他模块中之前训练时学到的知识就可以被更好地保留)。这个结构也和因果学习中的局部干预(localized intervention)有相似性(因果学习中认为我对一个变量做干预后,应该只对相邻的变量产生局部的影响,而不是对所有其他变量都产生影响)。
因此本文的主要动机是提出一套方法来从高维观测中学到倾向于用多个独立的机制的组合来完成任务的表征。本文提出的网络结构如下:

每一个蓝色/白色的方块表示一个循环独立机制(RIM,即一个子网络),对于每一个输入,首先用soft-attention判断输入和每一个RIM的相关性,并只选择相关性高的RIM(蓝色方框)输入。输入后RIM的状态会发生改变,同时产生输出。 此时,不同的被激活的RIMs之间还允许交流,同样是先对每一个RIM,判定有哪些其他RIM的信息是相关的,可以进行交流(指向橙色圆点的黑色实线)。在经过与其他的相关RIM的交流之后,更新当前RIM的状态并产生输出。
实验部分:
- 复制实验:输入一段序列,紧接着一长段零向量,再要求输出最初的序列。实验表明RIM可以从零向量长度50泛化到200(这也算泛化吗?),都能完成任务。
- RIM泛化的原理是环境变化时,输入的改变只会激活部分模块,而不是整个网络,所以其他部分依然是稳定的。此时本文做了一个识别MNIST序列任务,并泛化到不同分辨率的环境下。
- RL环境下,该文章以采用LSTM处理数序列的方法作为baseline,用RIM代替LSTM作为实验组,并用PPO算法学策略。
Inductive Biases for Deep Learning of Higher-Level Cognition
一个有趣的假设是人类级别的认知能力是可以由几个简单的原则所概括/解释的,如同真实世界是遵循着有简单的物理学规律的。基于这个假设,如果我们可以找到这些最基础的原则(归纳偏置,inductive biases)并让AI掌握这些原则,就可以像人类一样具有很强的泛化能力。过去的研究已经探索了很多归纳偏置,这篇文章主要总结了这些归纳偏置,并讨论了哪些归纳偏置最有利于实现类人的AI性能。
本文的主要假设是,深度学习以往的成功离不开好的归纳偏置,但想要获得好的泛化性能(在OOD的场景下),还需要添加更多/关键的归纳偏置。首先,人类的规律是直觉性的,隐式的;而我们需要的归纳偏置得是明确的,具体的。因此想要引入人类认知的规律必须要先引入更多的关于因果的符号和概念。其中包括我们不能再把数据看作是来自IID的分布,而是应该看成是一个非静态的过程产生的数据。
同时本文对于以往常用的归纳偏置做了总结:

关于归纳偏置的一些总结
在算法中引入归纳偏置有很多种形式,包括显示的损失函数、框架性的约束、参数共享、优化方案的选择等等。另一方面,有一些归纳偏置会以数据集的设置(e.g., 数量的多少)的形式出现(e.g., 更多的训练数据可以弥补归纳偏置/先验分布的缺失)。另外,有些归纳偏置带来的好处和改进参数优化过程带来的好处是一致的。
经典的机器学习框架都是基于IID假设的,基于IID我们才可以对泛化误差进行评估和求界。但现实问题往往都不是IID的。为了在变化的环境/任务下学习,我们要关注环境的变化规律/或者做合理的假设:1. 什么是不变的;2. 变化的部分是如何变化的。
我们可以把学习环境分成两个部分:缓慢学习不变的规律+快速学习变化的部分。这两个部分可能是不同的时间尺度上的学习。
系统性的泛化(systematic generalization)可能是一种适用于OOD的泛化,因为其可以系统性地从已掌握的概念中衍生出新的概念。
从人的认知角度看,人在新情景下会采用一种非习惯性的认知模式,与旧情景的认知模式完全不同。在认知到新事物后,新事物又会转化成已被认知的旧事物,用习惯性的认知模式去处理。本文整理了一些尚未被充分使用,但可能对OOD泛化有用的归纳偏置。
过去的机器学习方法具有一个归纳偏置:所有的模块/元素总是全程激活/运行的,但实际上,
面对不同的任务,我们可以只激活网络的部分模块
同样,每个模块也只选择其关心的信息作为输入。此时,未激活的模块可以视作处于习惯性认知模式(慢学习),而激活的模块视作非习惯的认知模式(快学习)。举个例子,预测台球桌上的移动:未碰撞时处于一种简单的模式,发生碰撞时处于一种复杂的模式。 但是对模块的设置是有无数种可能的,我们此时可以考虑从因果的角度去设置模块。
在因果当中有一种独立机制,即改变其中一个变量,只会导致少数相邻/相关变量的改变,而其他变量都不会改变。因此我们的一种归纳偏置就是
希望学到的各个模块之间的联系尽可能稀疏,或者说尽可能稳定,不容易受数据的扰动而发生太多改变。
环境的变化/数据分布的变化可能来自于什么?有两个主要的来源:1.环境的dynamics还未收敛到一个稳态分布(例如玩一个新游戏,玩家尚未掌握技巧,在游玩过程中不断改变自己的玩法);2.来自智能体的因果干预(例如关闭了一扇不能再打开的门,推箱子游戏中推到了角落)。人类的语言能有非常简短的词语来描述这些改变,这似乎给我们提供了一种归纳偏置:
在理想的表示空间中,大部分的改变都是局部起效的,即改变只会引起局部的变量/机制发生修改。
那些确定依赖关系的独立机制可以是一般/普遍的(generic),即以前是if A, then B;而我们希望是for all X,if f(X), then g(X)。
人脑可以把感知的信息分割成有含义的事件,并且可以选择性地回忆起很早之前的事件并建立联系。这个带来的归纳偏置是
因果链可以由时间上相距很远的短因果链串联起来。
-
Review of Causal RL
Causal Inference Q-network
Causal Inference Q-network: Towards
This paper learns invariant representation of perturbated observations.
Intrumental variables for offline RL
Instrumental Variable Value Iteration for Causal Offline Reinforcement Learning
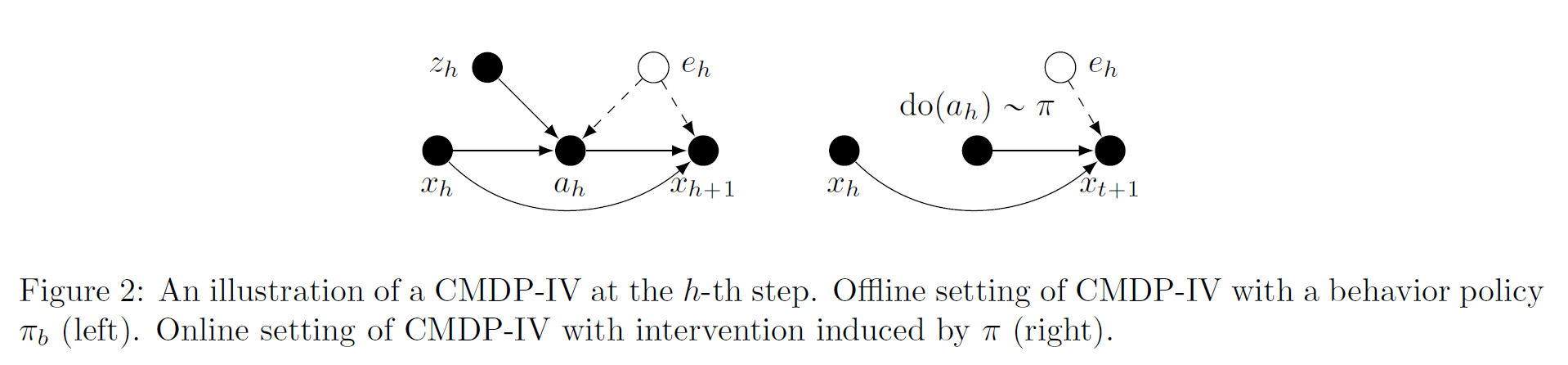
This paper supposes an observable $z_t$ as the instrumental variable that affects the action $a_t$ jointly with state $x_t$. The difference between $x_t$ and $x_t$ is that $z_t$ affects the $x_{t+1}$ only through $a_t$. For example, $a_t$ is the treatment, $x_t$ is the current health status and $z_t$ is the physician’s preference for treatments.
But what’s the advantage of introducing such structure? It calculates $\hat{x}’=f(x’,a\mid z)$
RL with confounders
Deconfounding RL in observational settings
This paper considers an unobserved factor $u$(confounders in causal learning) that affects observations, actions and rewards.
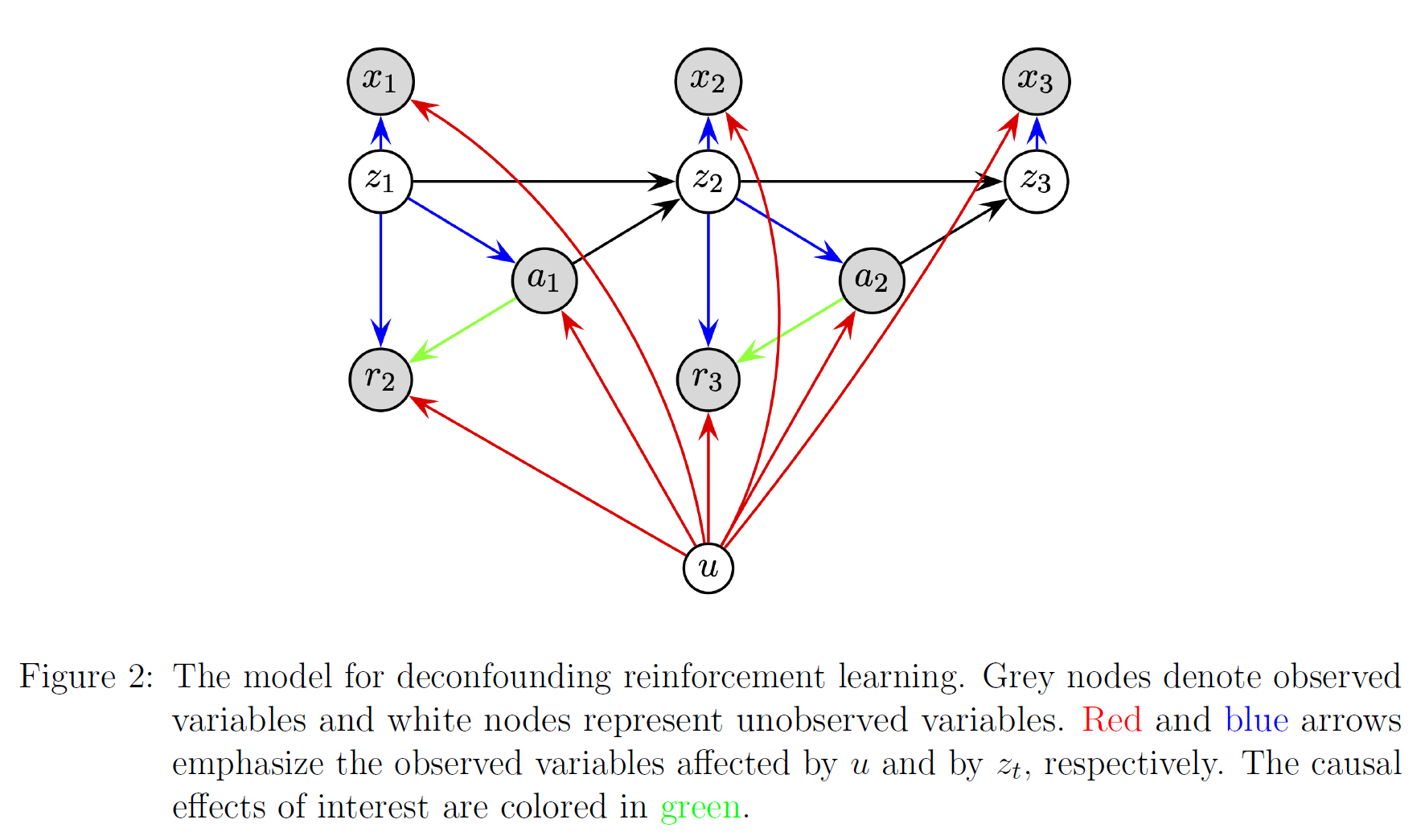
And it uses VAE to build an inference model for predicting $x_{t+1}$ based on $(x_t,a_t)$ and $z_t$.

I am puzzled that how and why the $u$ can be a time-independent confounder.
In experiments, it provides a confounding benchmark where the action space is divided and $u$ decides which partition of the action space is avaliable. It assumes that $u$ influences the reward function and observations but estimate the reward and action without $u$. So I am confused about the $u$.
Markov Decision Processes with Unobserved Confounders: A Causal Approach

The main difference between MDP and MDPUC is that the value function is conditioned on the actual action $x’_t$ when evaluating the $v(s_t)$ and $q(s_t,x_t)$ ($x_t$ is the potential action).

WOULDA, COULDA, SHOULDA: COUNTERFACTUALLY-GUIDED POLICY SEARCH
This paper introduces unobserved variables in POMDP by $s_{t+1}=f(s_t,a_t,u_t)$.
And Counterfactual Inference (CFI) uses following method:

It uses data to attain posterior distribution of $u$ and re-computer the target value under estimation $\hat{u}$.
Counterfactual Off-Policy Evaluation with Gumbel-Max Structural Causal Models (ICML19)
This paper introduces a class of SCMs to generate counterfactual trajectories in POMDP.

Cannot understand the example in section 3.1.
It defines the Counterfactual Stability, which means that in a categorical SCM if an intervention $I’$ increase the probability of oobserved state $i$ compared with the intervention $I$, then we can only observe $i$ under $I’$.

Off-Policy Evaluation in Partially Observable Environments
This paper defines Decoupled POMDP, where $(u,z)$ represents observed and unobserved states.
-
Review of Distributional RL
Introduction
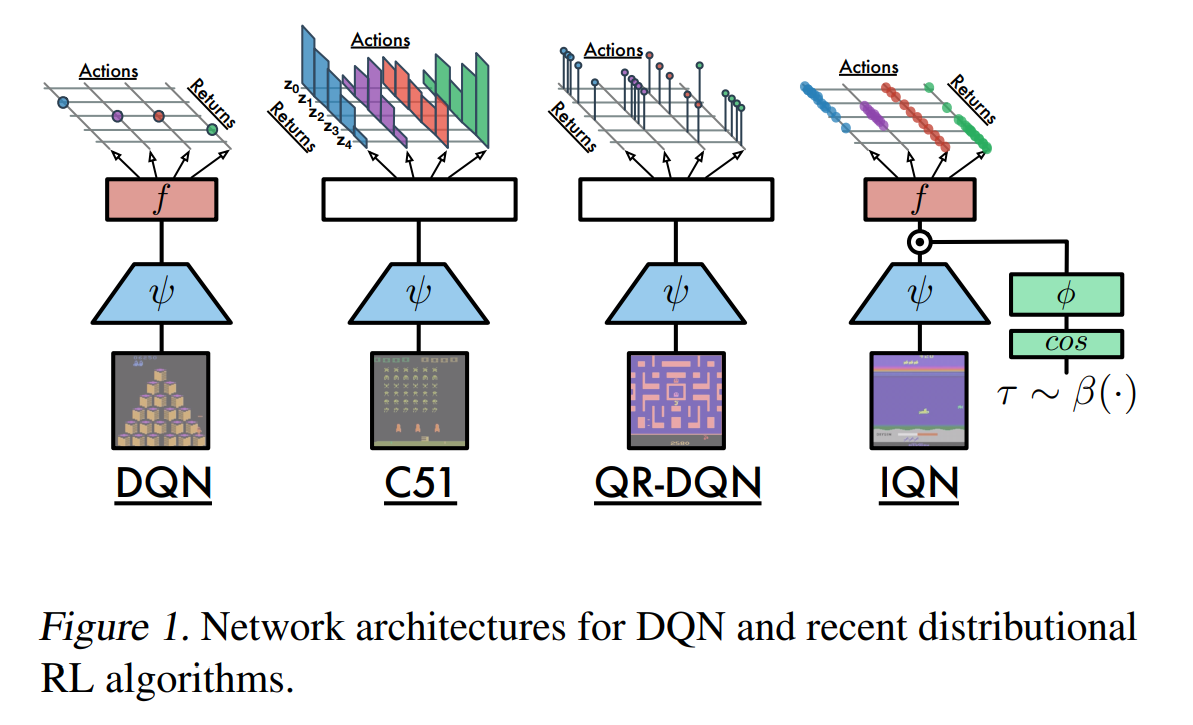
C51 & QR-DQN
Paper: A Distributional Perspectiveon Reinforcement Learning Paper: Distributional Reinforcement Learning with Quantile Regression
These two have been introduced in former reading notes.
IQN
Paper: Implicit Quantile Networks for Distributional Reinforcement Learning (ICML 2018)
A key improvement of IQN is the expanding from fixed quantiles ${\tau_i}_{i=1}^N$ to parameterized quantiles $\tau \sim U(0,1)$. The q-values of quantiles are updated by sampled $\tau$ and $\tau’$:

With parameterized quantiles, IQN can approximate the whole continuous distribution.
What’s more, another important improvement is that we can apply the utility function into distributional q-values, which can be achieved by distorted sample $\beta(\tau)$ where $\beta:[0,1]\to [0,1]$.
The choice of $\beta$ includes risk-neutral, risk-averse and risk-seeking. A special example is conditional value-at-risk (CVaR):
\[CVaR(\eta,\tau)=\eta\tau,\]which changes $\tau \sim U(0,1)$ to $\tau \sim U(0,\eta)$ for guaranteeing performance on worse conditions.
A special trick of embedding the quantile $\tau$ is widely used in Distributional RL:
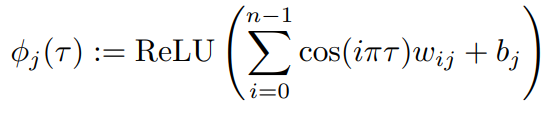
FQF
Paper: Fully Parameterized Quantile Function for Distributional Reinforcement Learning
The main contribution of this paper is the parameterized quantiles $\tau(\theta)$ while in IQN the quantiles are sampled from a distribution. FQF projects the quantile function into a staircase function:
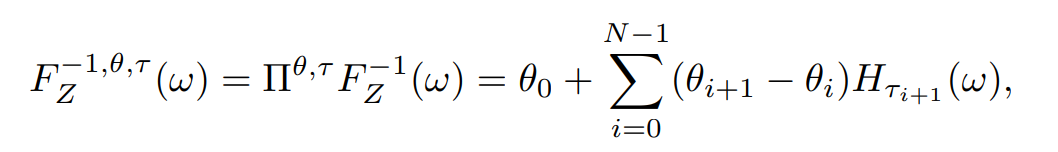
and find the staircase function with minimal 1-Wasserstein loss:
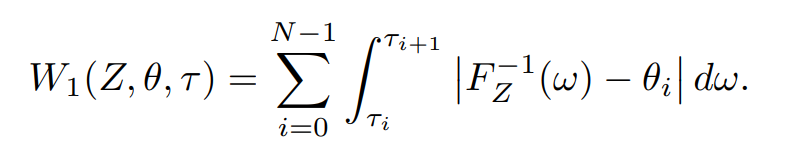 .
.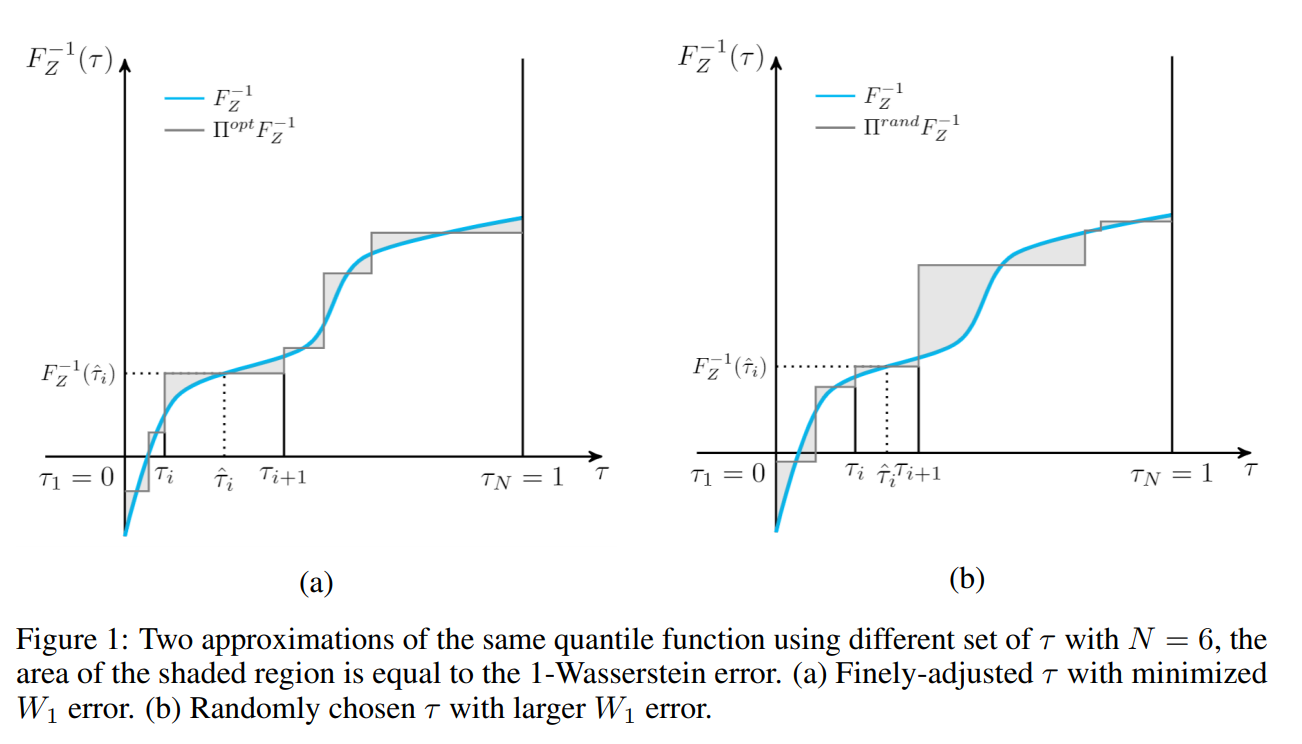 .
.Non-crossing QR-DQN
Paper: Non-crossing quantile regression for deep reinforcement learning
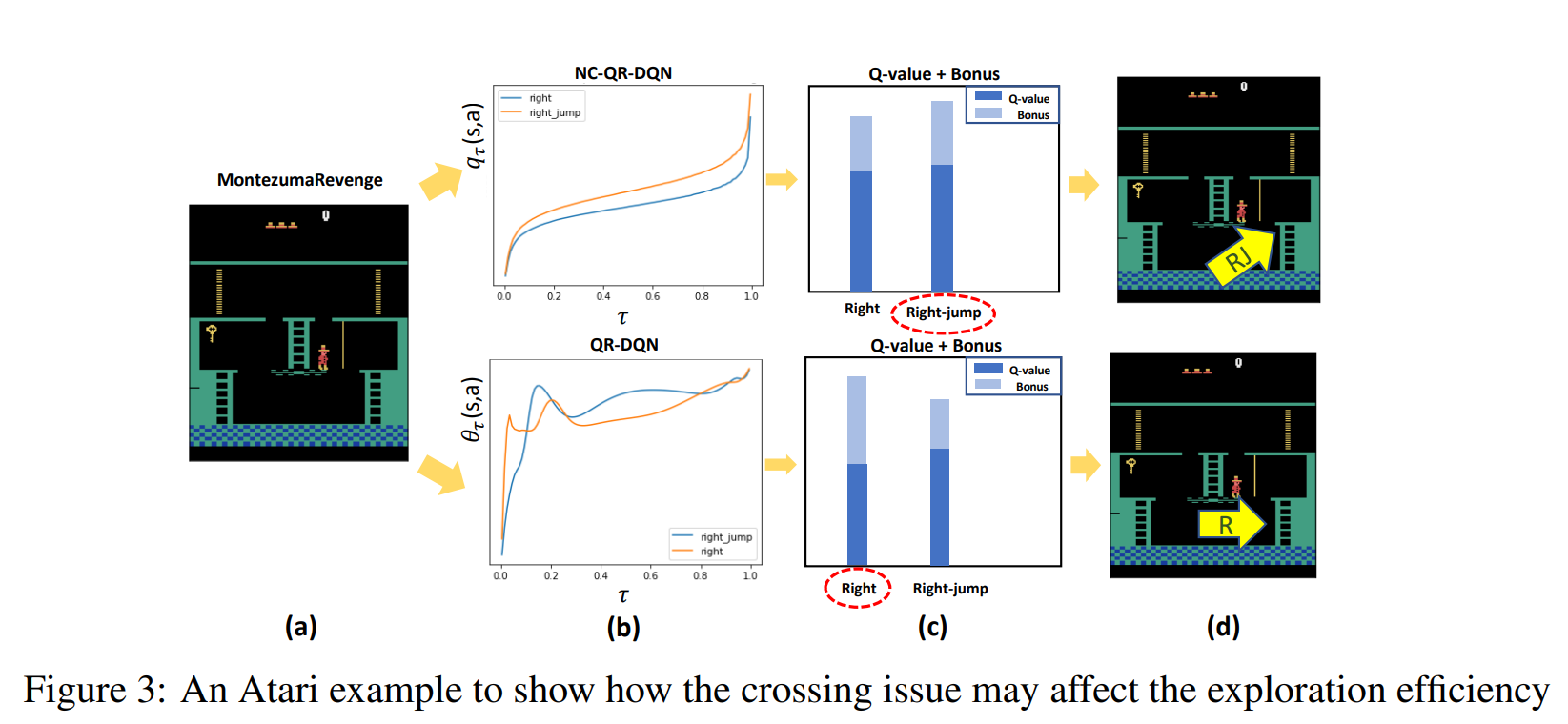
Experiments show that quantile regression cannot guarantee the non-decreasing property of learned quantiles.
The constrained optimization is:
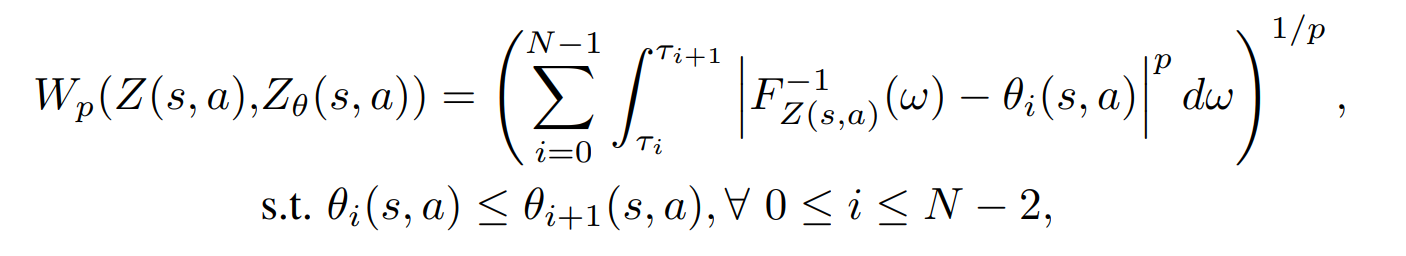 .
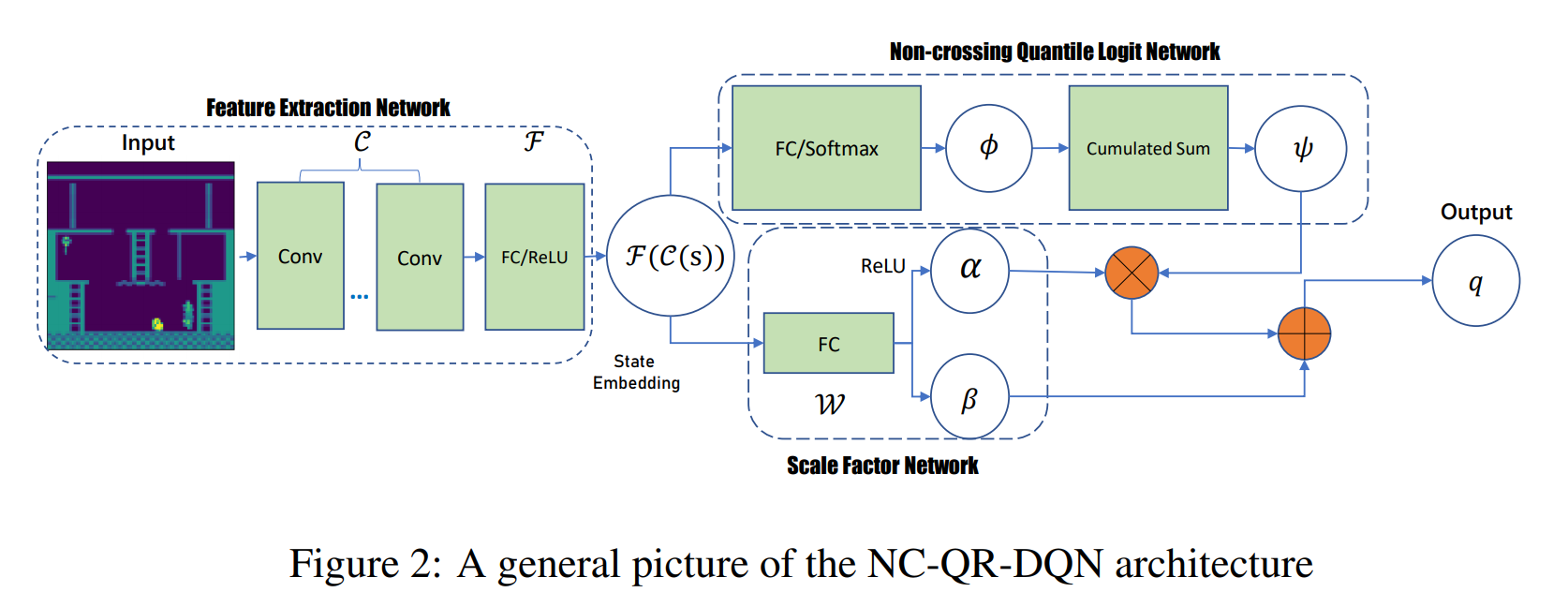
.To solve this problem, NC-QR-DQN search for a subspace of initial Z-space that $Z_Q\in Z_\Theta$. quantile functions $Z_q={\theta_i}_{i=1}^N$ in $Z_Q$ are all satisfying the non-decreasing constraint.
In another perspective, solving this optimization problem is equivalent to finding a projection operator $\Pi_{W_1}$ such that:
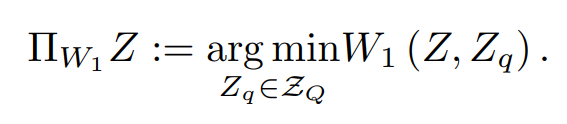 .
.In practice, it uses a network to produce the $\phi_{i,a}$ (the i-th quantile value for action $a$ given a state) and then re-computes the outputs by $\psi_{i,a}=\sum_{j=1}^i \phi_{j,a}$ where $\psi_{N,a}=1$ and $\psi_{i,a}$ is non-decreasing. Since $\psi\in [0,1]$, there is another scale network to recover the logits in $[0,1]$ to the original range with :
\[q_i(s,a) =\alpha(s,a)*\psi_{i,a}+\beta(s,a)\]And the modified TD error is $\delta_{i,j}=r+\gamma q_j(s’,a^)-q_i(s,a)$ where $a^=\arg\max_{a’}\sum_{j=1}^N q_j(s’,a’)$.
 .
.By the way, the precise estimation of truncated variance by including the non-cross constraint can help measure the intrinsic uncertainty.
 .
.DLTV
Decaying Left Truncated Varianc–a novel exploration strategy that more sufficientli utilize the distributional information. The key idea is that the quantile is usually assymmetric and the upper trail variability is more relevant. There is an upper truncated measure of the uncertainty:
\[\sigma_+^2=\frac{1}{2N}\sum_{i=N/2}^N(\tilde{\theta}-\theta_i)^2 \\ c_t=c\sqrt{\log t/t}\\ a^*=\arg\max_{a'}(Q(s,a')+c_t\sqrt{\sigma_+^2})\]where $\tilde{\theta}$ is the median rather than mean.
Expectile Distributional RL (EDRL)
Paper: Statistics and Samples in Distributional Reinforcement Learning
In this paper, the algorithms of distributional RL can be decomposed into following steps:
- Find a series of statistics to discrib the distribution (e.g., the discrete or continuous quantiles)
- Find a rule to update/re-compute those statistics and get losses.
Previous distributional RL can be divided into two types:
1.Categorical DRL: $\eta(x,a)=\sum_{k=1}^Kp_k(x,a)\delta_{z_k}$ and learns weights with fixed quantiles $z_k$
2.Quantile DRL: $\eta(x,a)=\frac{1}{K}\sum_{k=1}^K\delta_{z_k(x,a)}$ and learns the new $\tau_k=\frac{2k-1}{2K}$ quantiles by minimizing the quantile regression loss: \(QR(q;\mu,\tau_k)=\mathbb{E}_{Z\sim\mu}[[\tau_k\mathbb{I}_{Z>q}+(1-\tau_k)\mathbb{I}_{Z\geq q}]\mid Z-q\mid]\)
This paper proposes the ``expectation quantile’’ (expectiles):
\[ER(q;\mu,\tau_k)=\mathbb{E}_{Z\sim\mu}[[\tau_k\mathbb{I}_{Z>q}+(1-\tau_k)\mathbb{I}_{Z\geq q}]\mid Z-q\mid^2]\]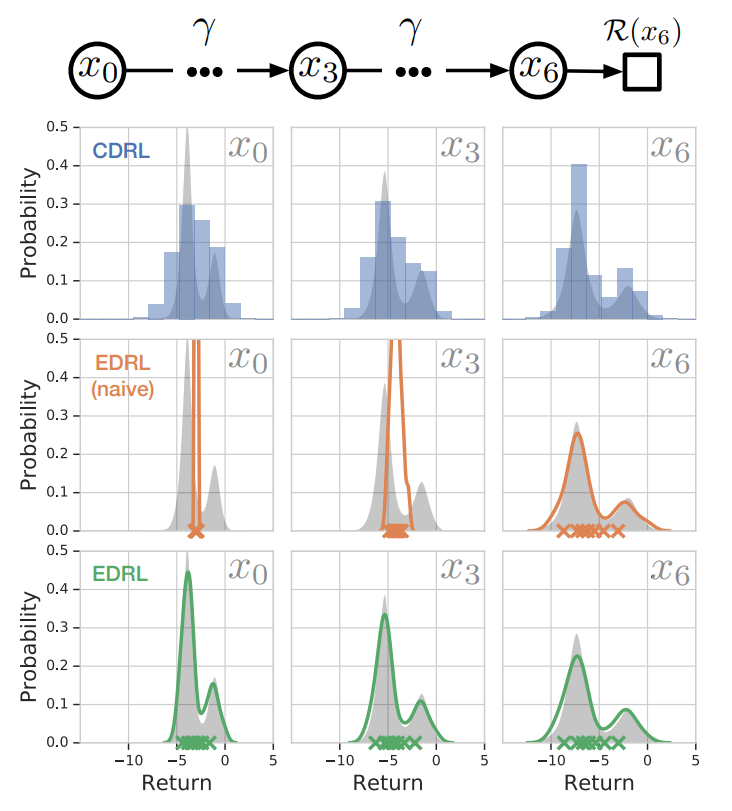 .
.CDRL overestimates the variance because the projection splits the probability mass across the discrete support. In contrast, EDRL(naive) only replaces the quantiles with expectiles and underestimates the variance.
There is a crucial problem that the learned $z_k(x,a)$ have the semantic of a statistic, but in updating, $z_k(x,a)$ in $(\Tau^\pi\eta)(x,a)$ have the semantic of both statistics and samples
To solve this problem, EDRL seperates the bellman updating process into two parts:
1.learn statistics (expectiles) from the recovered distribution/samples;
2.Recover the distribution from learned statistics.
 .
. .
. .
.quantiles and expectiles
quantiles and expectiles correspond to the concept of median and mean. In the regression perspective of the median and mean, it can be viewed as the solution of an optimization problem under different norm:
1.$\textbf{median}[y]=\arg\min_{m\in\mathbb{R}}[\frac{1}{n}\sum_{i=1}^n\mid y_i-m\mid]$
2.$\textbf{mean}[y]=\arg\min_{m\in\mathbb{R}}[\frac{1}{n}\sum_{i=1}^n(y_i-m)^2]$
Correspondingly, given risk functions:
1.$\mathcal{R}_\tau^q(u)=\mid u\mid\cdot [(1-\tau)\cdot\mathbb{I}(u<0)+\tau\cdot\mathbb{I}(u\geq0)]$
2.$\mathcal{R}_\tau^e(u)=\mid u\mid^2\cdot [(1-\tau)\cdot\mathbb{I}(u<0)+\tau\cdot\mathbb{I}(u\geq0)]$
which is equivalent to weighted meadian/mean.
MMD-DQN
Paper: Distributional Reinforcement Learning with Maximum Mean Discrepancy
-
Notes of Causal Inference-3
In note 1, we introduce the identification-estimation flowchart. And in note 2, we introduce the corresponding concepts in graphs.
Now we will introduce causal models and data into prior identification-estimation flowchart:
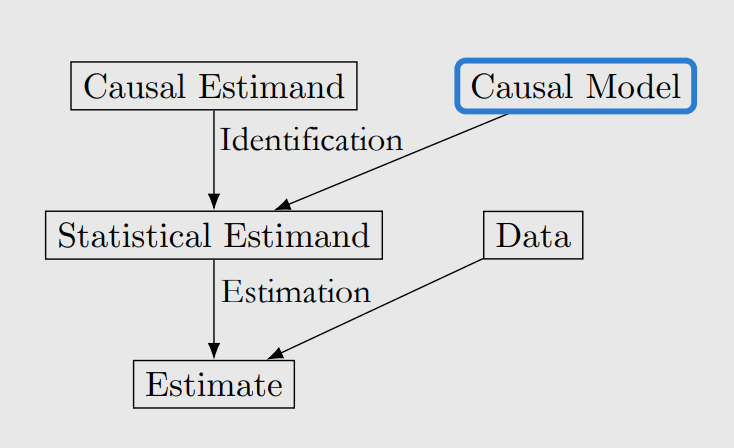
The $do-$operator
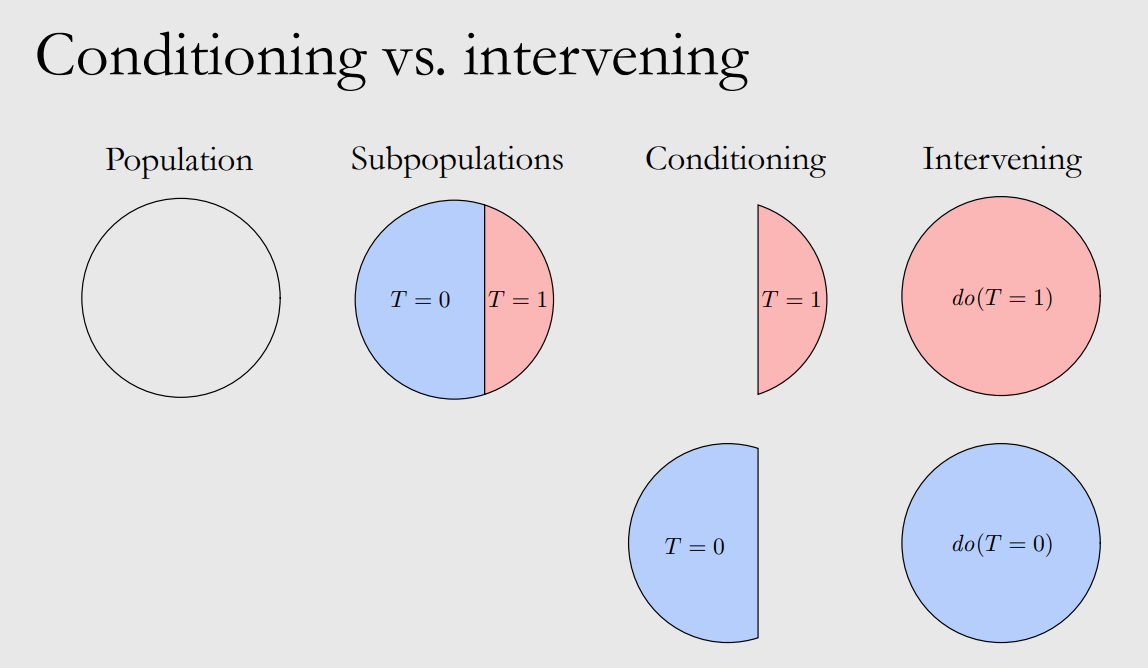
Firstly we differ the conditioning and intervening:
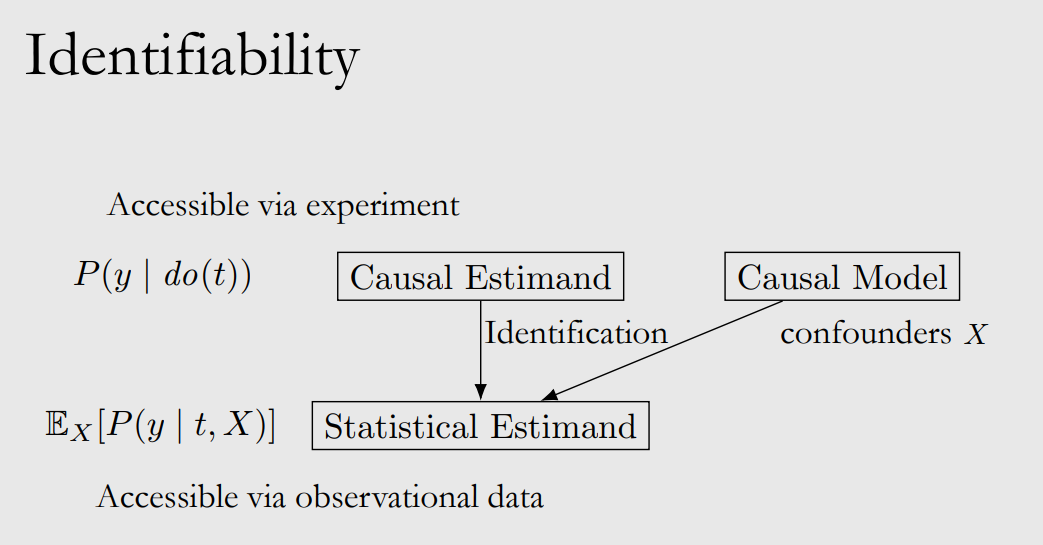
The main effect of introducing causal models is finding all the confounders $X$, by which we can have unconfounderness assumption and do identification:
Modularity assumption
Nextly, we introduce the modularity assumption:
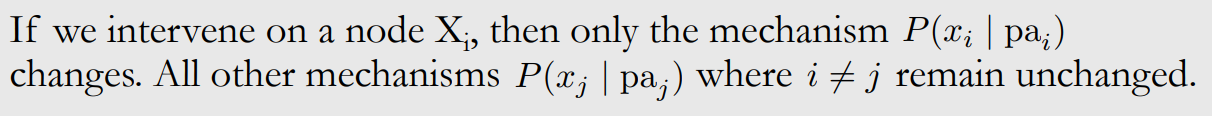
More formaly:

which means that

Take a simple example of identifying $P(y \mid do(t))$:

And then we can find the key difference between causation and association in formula:
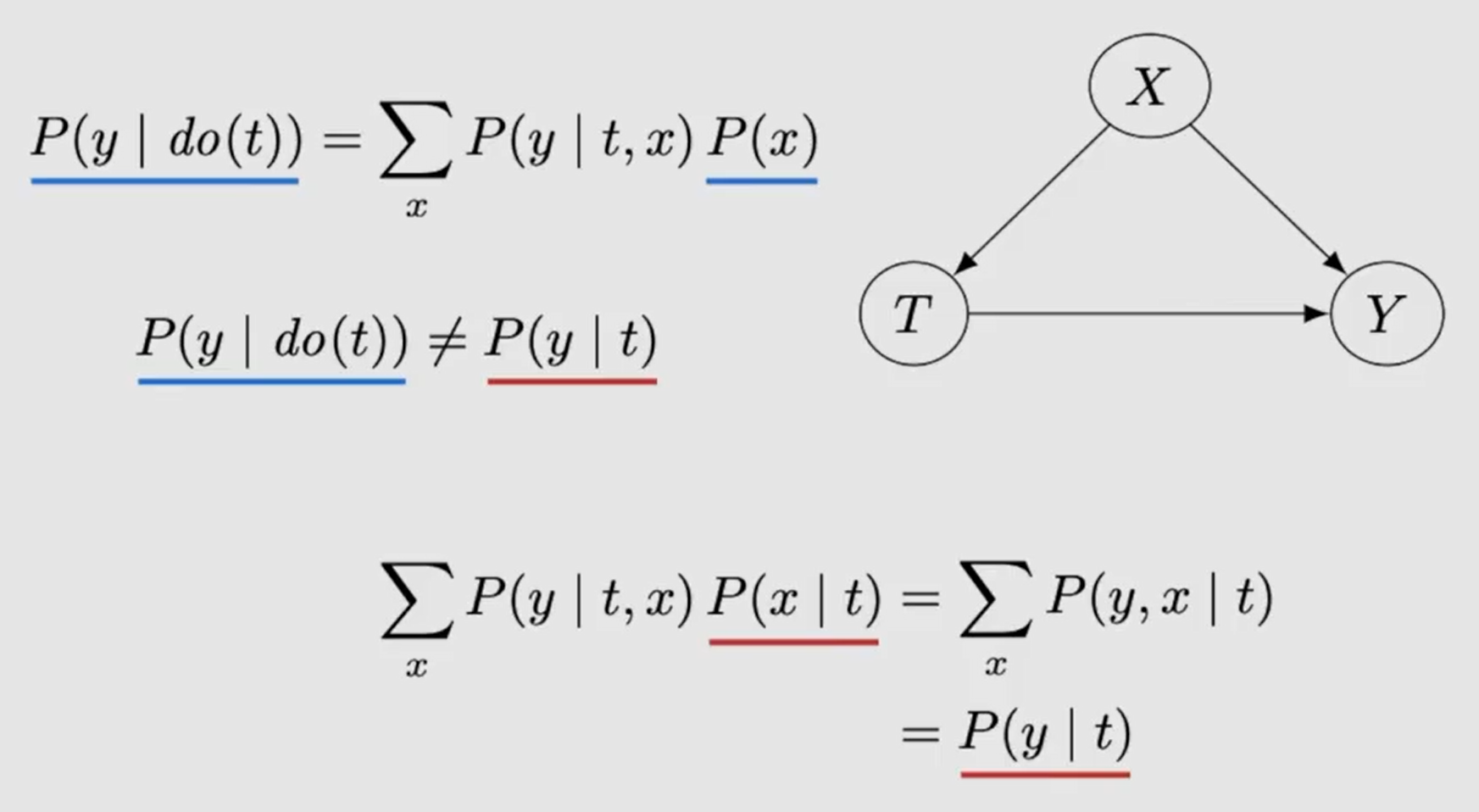
which is the sample probability over the confounderness $X$.
-
Notes of Causal Inference-2
Bayesian networks and causal graphs
Bayesian networks discrib statistical models (no causality):
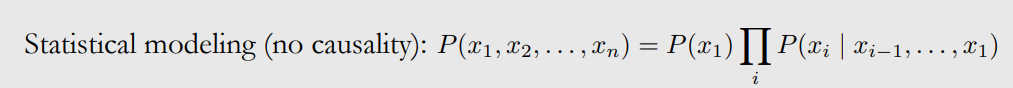
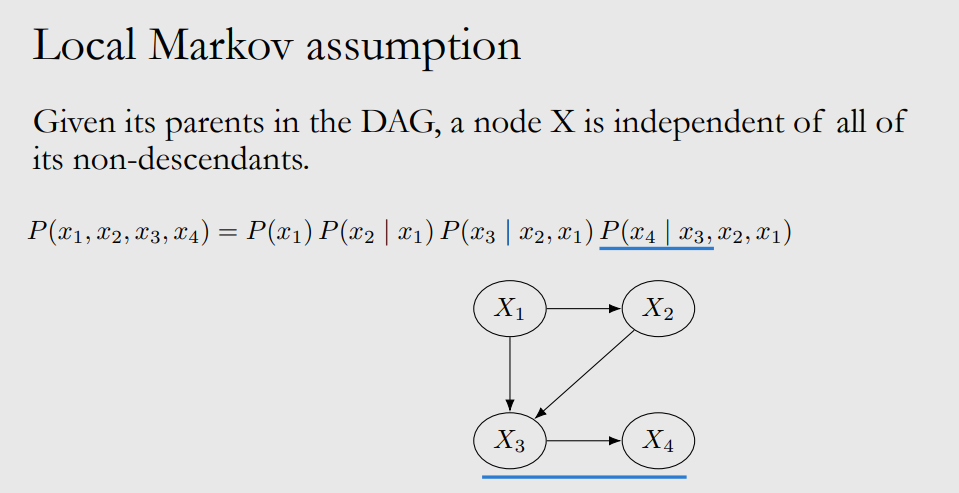
With local markov assumption, we can do bayesian network factorization:
Minimality assumption:

Causal edge assumption:
In a directed graph, every parent is a direct cause of all its children.
The Blocks in Graphs
Here we define the “blocks” in graphs, where the blocked path means $X$ and $Y$ are independent.
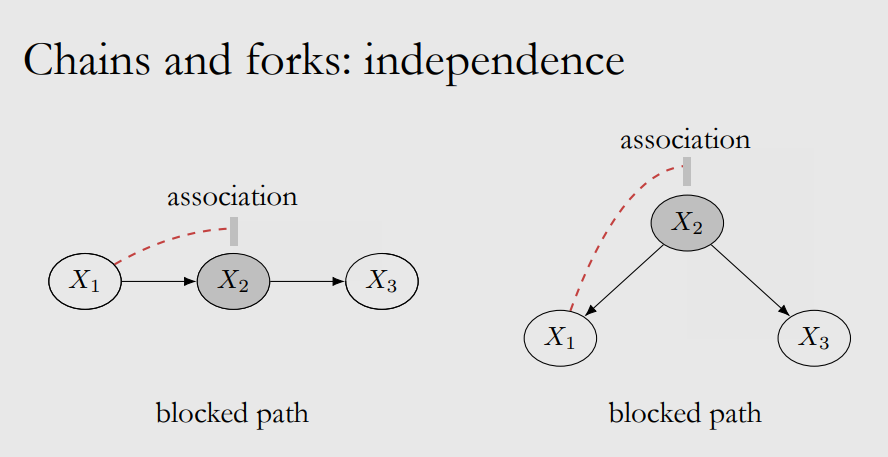
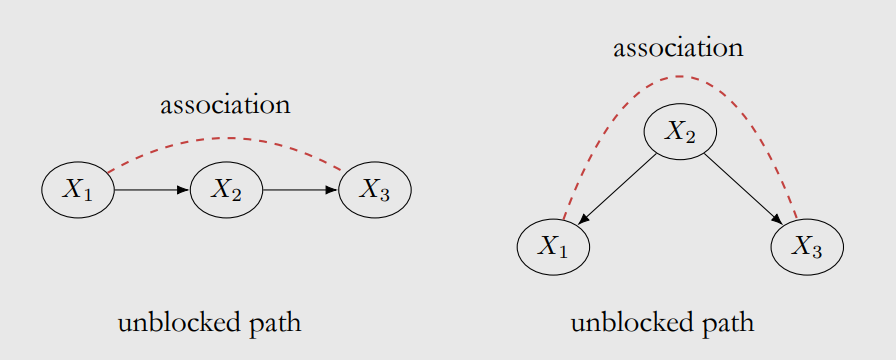
The proof is easy in chains:

However, things are different in immoralities, including its descentants:
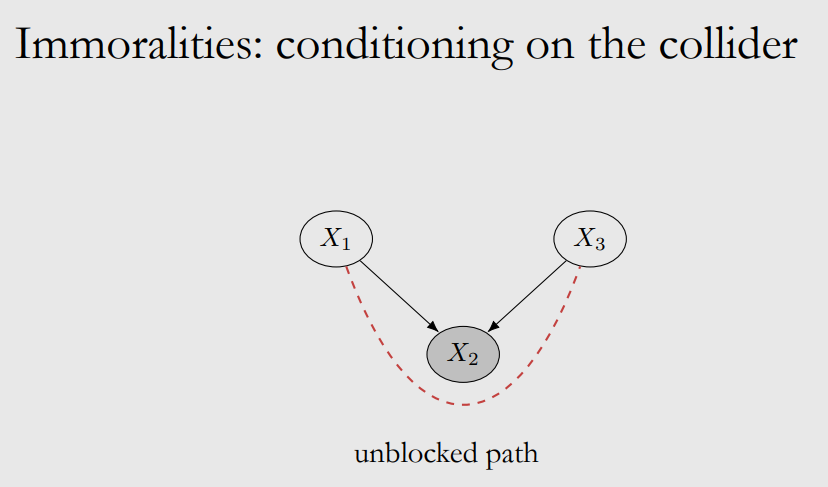
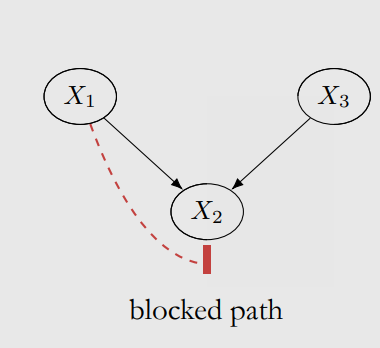
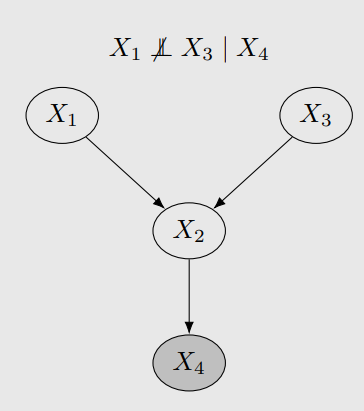
Here we define the “blocked path”:

And then we define “d-separation” based on the blocked path:

We can distinguish causal association and confounding asscociation with causal egde assumption:
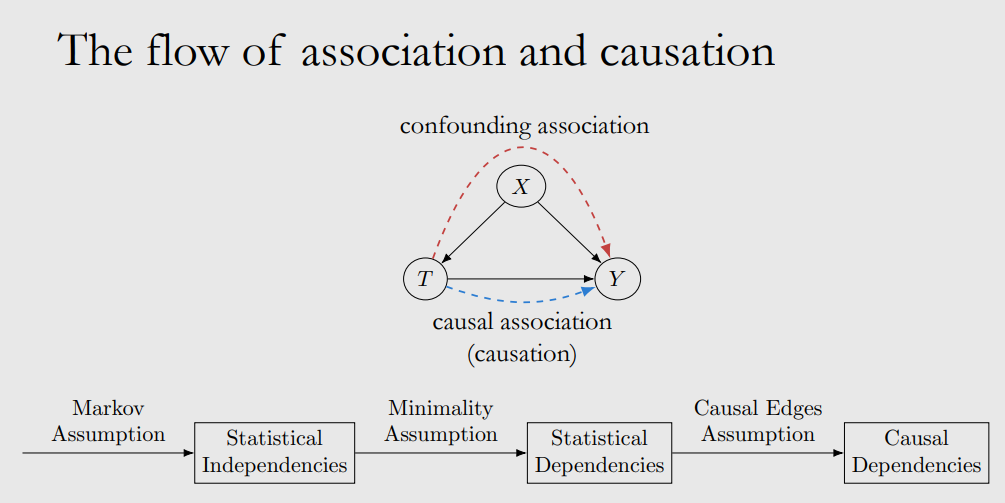
-
Notes of Causal Inference-1
- What Does Imply Causation?
- Identificability
- Assumption 1: Ignorability
- Assumption 1: Conditional exchangeability
- Assumption 2: Unconfoundedness
- Assumption 2: Positivity
- Assumption 3: No Interference
- Assumption 4: Consistency
- Summary
What Does Imply Causation?

Consider following example, we cannot take $Y_i \mid _{T=1} - Y_i \mid _{T=0}$ as the causal effect because $Y_i\mid _{T=1}$ cannot represent the potential outcome of “if we take $T=1$”.
The main difference between causation and correlation is $Y_i\mid _{T=1}\neq Y_i\mid _{do(T=1)}$
Here we calculate the true causal effect, $Y_i\mid _{do(T=1)}-Y_i\mid _{do(T=0)}$, noted as $Y_i(1)-Y_i(0)$:
\[\mathbb{E}[Y_i(1)-Y_i(0)]=\mathbb{E}[Y_i(1)]-\mathbb{E}[Y_i(0)]\\ \neq \mathbb{E}[Y_i\mid T=1]-\mathbb{E}[Y_i\mid T=0)]\]which is because we have confounding association $C$:
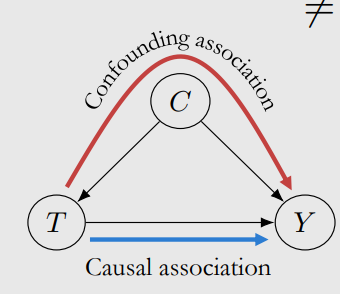
Identificability
Our goal is to calculate causal quantity with statistic quantity:

Assumption 1: Ignorability
The igorability can be showed as following: \(\mathbb{E}[Y(1)]-\mathbb{E}[Y(0)] = \mathbb{E}[Y(1)\mid T=1]-\mathbb{E}[Y(0)\mid T=0)]\)
which means that the potential outcome $Y(1)$ is regardless of what the $T$ value is in practice. In the following table, the blankets in $Y(1)$ and $Y(0)$ columns are the unobservable outcomes. Those values are independent of whether corresponding $T$ is taken.
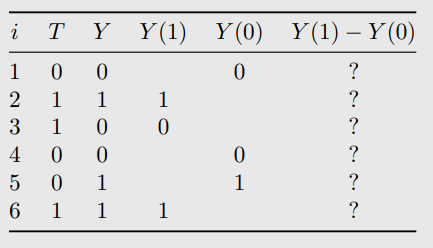
The ignorability can be described as:
\[(Y(1),Y(0)) \perp \perp T\]Well, in another perspective, the ingorability can be viewed as exchangeability:

which means that the outcomes is independent of what data you choose (swaping A and B doesn’t changes the expectations $y_0$ and $y_1$).
Assumption 1: Conditional exchangeability
However, we don’t know whether the data set satisfies exchangeability. Looking at the following example, we find that the distribution of “drunk/sober” in $T=1$ is different from it in $T=0$, where exchangeability is not satisfied.
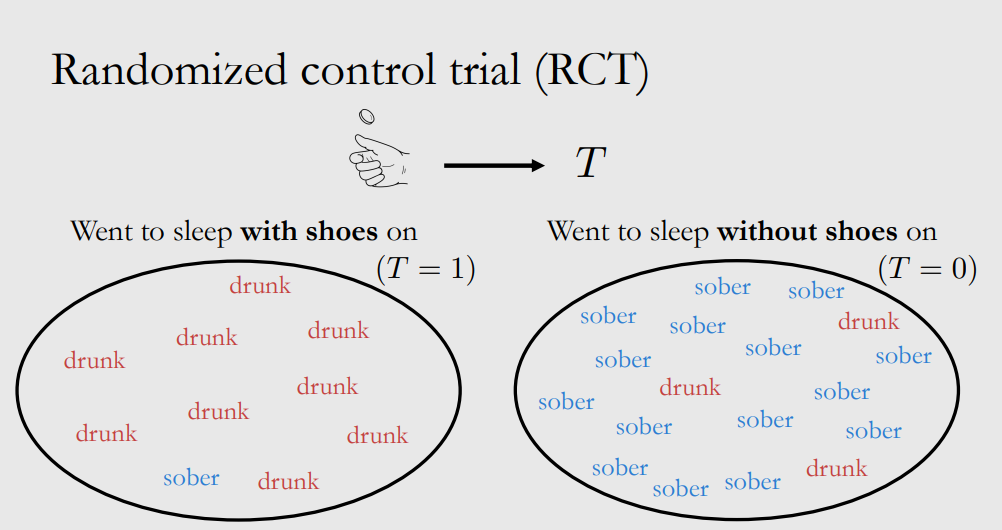
So the conditional exchangeability is proposed that $(Y(1),Y(0))\perp\perp T\mid X$, where $X$ represents “drunk/sober”. So we have:
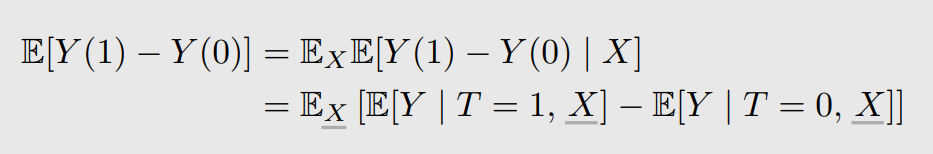
Assumption 2: Unconfoundedness
Unconfoundedness is an untestable assumption that $X$ is the only confoundedness and there is no unobservable “W”.
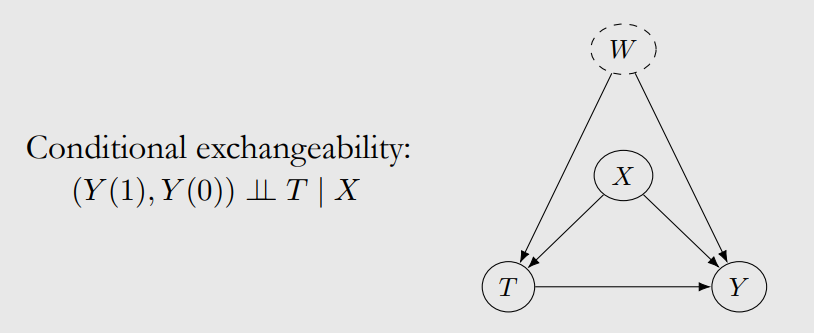
Assumption 2: Positivity
Positivity demands that the support set is consist of the set $X$.

And if we don’t have positivity, we have to predict the potential outcomes:
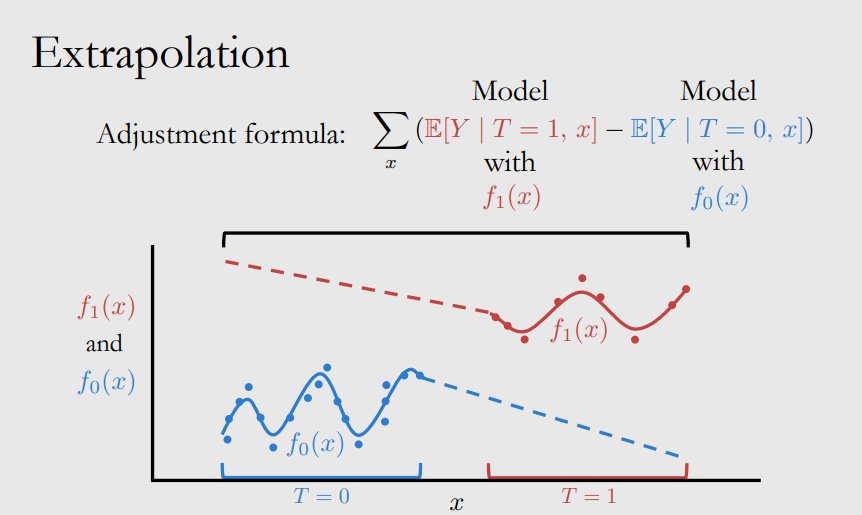
Assumption 3: No Interference
No interference means that the choice of $T$ in other samples doesn’t influence this outcome:
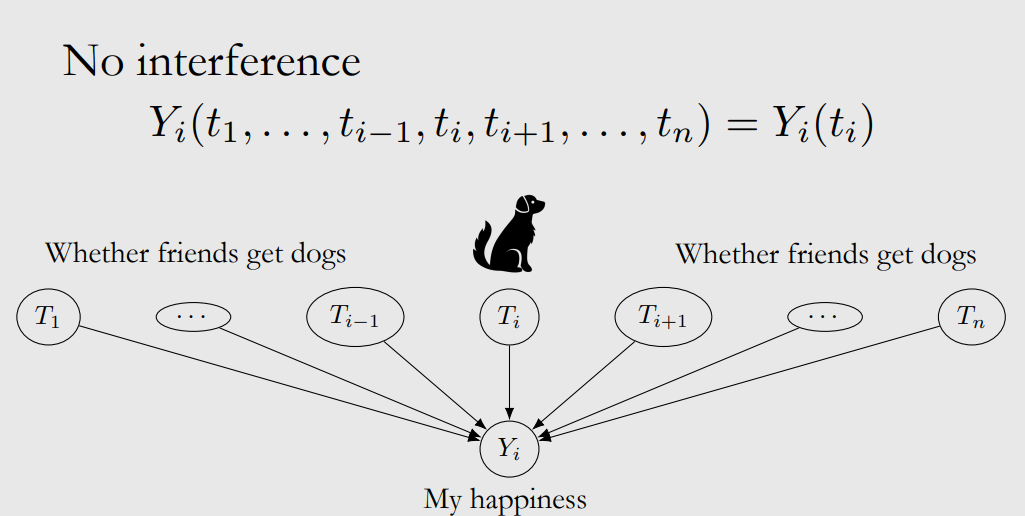
Assumption 4: Consistency
The same $T$ must correspond to the same outcome.

Summary

-
Notes of CS598
Notes of CS598
Value Iteration
Note $\mathcal{T}$ as the bellman optimal operator and $Q^*$ as the optimal Q-function that:
\[(\mathcal{T} Q) (s,a) = R(s,a)+\gamma \mathbb{E}P(s'|s,a)[\arg\max_{a'}Q(s',a')]\] \[Q^*=\mathcal{T} Q^* (bellman \ optimality \ equation)\]Similarly, \((\mathcal{T}^\pi Q) (s,a) = R(s,a)+\gamma \mathbb{E}P(s'|s,a)[Q(s',\pi(s')] \\ Q^\pi=\mathcal{T}^\pi Q^\pi\)
Planning
Assume we know the DMP model, then we can do planning: compute $V^,Q^$ given $\mathcal{M}$ by value iteration and policy iteration.
We have the algorithm that, \(Q^{*,0}=Q_0\\ Q^{*,h}=\mathcal{T} Q^{*,h-1}\)
-
trust region policy optimization 阅读笔记
-
概率论(4)
第三章 数字特征与特征函数
-
概率论(3)
第二章 随机变量与分布函数