论文题目: Lipschitz Continuity in Model-based Reinforcement Learning
简介
本文的主要工作是给出了满足”Lipschitz连续”性质的模型中多步预测的误差界和值函数估计的误差界。
基础概念
基于模型的强化学习(model-based RL)
RL问题一般都从马尔科夫决策过程视角来看待,以五元组$<S,A,R,T,\gamma>$表示一个RL系统,而基于模型的强化学习方法就是估计 \(\hat{T}(s'|s,a)\thickapprox T(s'|s,a) \ \ \ \hat{R}(s,a)\thickapprox R(s,a)\)
Lipschitz 连续

考虑到转移函数$T$的定义域为状态集$S$与动作集$A$的联合,我们进一步定义在动作集A上的一致Lipschitz连续:
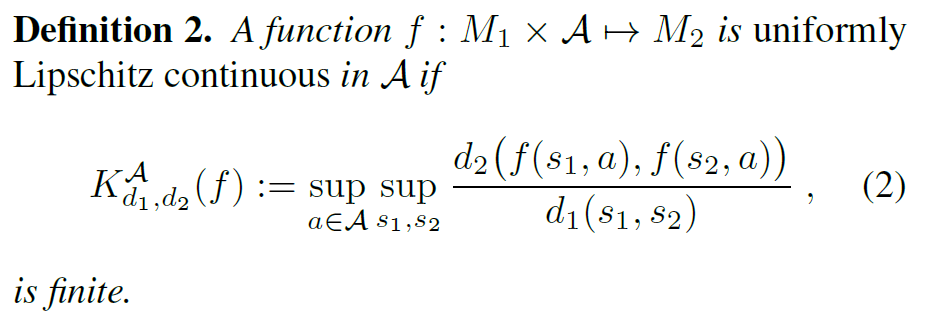
W度量(Wasserstein Metric)
前面的定义中,$f(s,a)$之间的距离并没有定义,实际上$f(s,a)$是一个分布,所以我们需要定义分布之间的距离。下面介绍W度量:

直观地说,W度量衡量的是从分布A变换到分布B所需的最小代价,这里的$j$可以理解成一种“分布A中采样点到分布B中采样点的一一映射关系”,在这种给定的映射关系下,$(s1,s2)$二元组的出现概率/联合密度函数。
举个例子说明,随机变量$x$的分布情况是$P(x=0)=1/2, \ P(x=1)=1/4, \ P(x=2)=1/4$
随机变量$y$的分布情况是
$P(y=0)=1/4, \ P(y=1)=1/2, \ P(y=2)=1/4$
当我们取足够多的样本($N$)后,对于$x$,会有$N/2$个点落在0,$N/4$个点落在1,$N/4$个点落在2;
对于$y$,会有$N/4$个点落在0,$N/2$个点落在1,$N/4$个点落在2。
如果我们采用的映射关系为把$x$中的0,1,2分别映射到$y$中的1,0,2,那么联合密度函数$j()$就是$j(0,1)=1/2, \ j(1,0)=1/4, \ j(2,2)=1/4$,其余均为零。这时总距离为$1/2|1-0|+1/4|0-1|+1/4*|2-2|=3/4$。
但这并不是最小的,最小的距离是$1/4|1-0|+1/4|0-0|+1/4|1-1|+1/4|2-2|=1/4$,映射关系为将$N/4$份$x=0$的样本点映射到$N/4$份$y=1$的样本点上,其余均为恒等映射(0到0,1到1,2到2)。
Lipschitz连续模型

这里不直接定义转移函数$T(s’|s,a)$的连续性,而是定义状态映射集$F_g$的连续性。$f$是一种状态空间的自映射,由$g$定义了$f$的条件分布。我们称$F_g$是Lipschitz连续的,当对于所有的$f \in F_g$,$K$都是有界的(这个连续性与$f$的分布无关,即与$g$无关)。
下面举个例子来说明:

$F_g$当中共有四个确定性的状态-状态转移函数,在不同的动作$a$下,这四个转移函数有不同的分布。这里对所有的$f$,$K$都不超过2,所以$F_g$满足上面定义的Lipschitz连续。
论文推理部分
n步转移误差界
首先基于上面的概念,我们可以用$g(f|a)$来表示转移函数: \(\hat{T}(s'|s,a)=\sum_f \Pi(f(s)=s')*g(f|a)\) 上式是先通过$a$确定$f$的分布,将那些能得到$s’$的$f$在$g(\cdot|a)$概率累加起来。
这也是一种很有意思的理解转移函数的方式。
传统方法是把$s,a$作为输入,$s’$作为输出,这就像是一张表格,横轴是状态,纵轴是动作;而这里是先把状态转移进行分类,不同的动作会对应不同的状态转移函数集的分布,就好比不同的状态转移函数是空间中的不同维度($dim_i=f_i()$),而不同的动作象征着从不同的视角去看待这个多维空间中的物体(状态转移关系),这个物体在各个维度的值(指代该维度对应的状态转移函数的发生概率)会随着视角(动作)变化而变化。
进一步,当前状态$s$为一个分布$\mu(s)$时,可以更一般地表示状态转移函数: \(\hat{T}_G(s'|\mu,a)=\int_s\sum_f\Pi(f(s)=s')g(f|a)\mu(s)ds\) 在此基础上我们可以定义$\hat{T}$的Lipschitz连续:
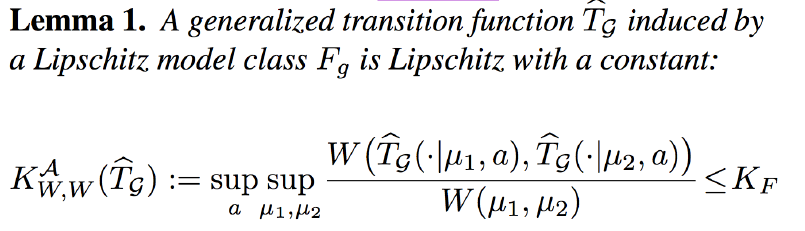
在定义了构建的转移模型$\hat{T}$后,可以回过头来再次解释为什么选择Wasserstein度量,以下图为例:
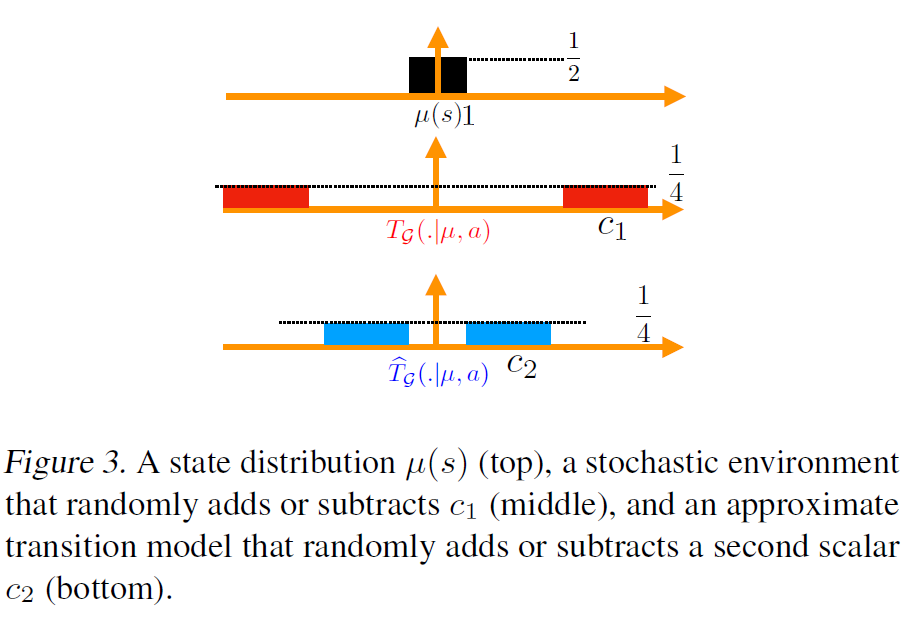
当前状态$\mu(s)$的分布如最上方的图,真实的转移如中间图,模拟的转移如最下方的图。
常见的分布距离度量有KL散度、全变分和W度量。
如果采用KL散度
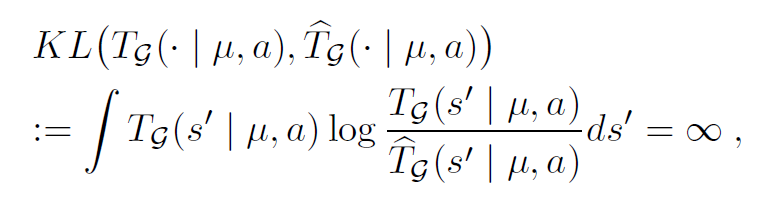
因为支撑集不同,在KL散度定义下会出现无穷大。
如果采用全变分
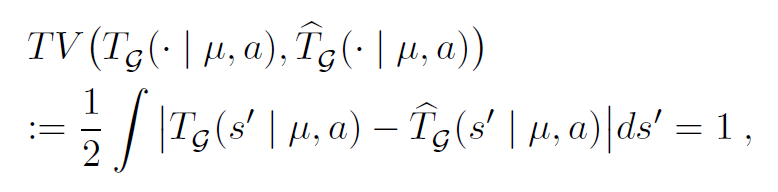
因为支撑集不同,所以会得到1
如果用Wasserstein度量
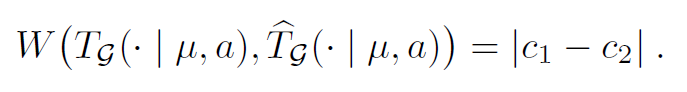
能正确反映$c_1,c_2$。
定义模拟的转移函数与真实转移函数的差距。

定义n步误差:

可以证明n步误差可以被真实转移函数和模拟转移函数的Lipschitz常数控制住

值函数误差界

这里定义了真实环境和模拟环境中的值函数估计。不过此处有很强的假设,要求动作空间只有一个$a$,同时回报函数只依赖于状态。
在此基础上可以给出值函数估计的误差界。

但要注意的是,这个误差界需要很强的假设,尤其是$\bar{K}<\frac{1}{\gamma}$,我们知道$\gamma$一般是个仅比1小一点的数,所以$\frac{1}{\gamma}$会比1只大一点点,这就对真实环境和模拟环境的Lipschitz连续性要求非常高。
小结
这篇文章是今年暑期研讨班钱鸿师兄介绍的,我之所以现在又回过头来总结这篇文章是因为其中对于转移函数$T$的模拟方法非常有意思,我感觉这对于我之后做状态抽象的研究会带来一些灵感。