Notes of CS598
Value Iteration
Note $\mathcal{T}$ as the bellman optimal operator and $Q^*$ as the optimal Q-function that:
\[(\mathcal{T} Q) (s,a) = R(s,a)+\gamma \mathbb{E}P(s'|s,a)[\arg\max_{a'}Q(s',a')]\] \[Q^*=\mathcal{T} Q^* (bellman \ optimality \ equation)\]Similarly, \((\mathcal{T}^\pi Q) (s,a) = R(s,a)+\gamma \mathbb{E}P(s'|s,a)[Q(s',\pi(s')] \\ Q^\pi=\mathcal{T}^\pi Q^\pi\)
Planning
Assume we know the DMP model, then we can do planning: compute $V^,Q^$ given $\mathcal{M}$ by value iteration and policy iteration.
We have the algorithm that, \(Q^{*,0}=Q_0\\ Q^{*,h}=\mathcal{T} Q^{*,h-1}\)
Q: If we denote $\pi_h:=\pi_{Q^{,h}}$ , and $Q^{\pi_h}$ be stationary point of operator $\mathcal{T}^{\pi_h}$ , then are $Q^{\pi_h}$ and $Q^{,h}$ equivalent?
A: No. This problem equals that assume a policy $\pi$ is derived from $Q$, then whether $Q$ must be equal to the converged Q-function $Q^{\pi}$. It’s obviously not.
Q: How good is the policy $\pi_{Q^{*,H}}$ ?
A: For arbitrary $f$, $|V^-V^{\pi_f}|_\infty=\frac{2 |f-Q^|_\infty}{1-\gamma}$
Q: Bound $|Q^{,H}-Q^|_\infty$ ?
A: Lemma : $|\mathcal{T}f-\mathcal{T}f’|\infty\leq\gamma|f-f’|\infty$
Prove: \(\|Q^{*,H}-Q^*\|_\infty=\|\mathcal{T}Q^{*,H-1}-\mathcal{T}Q^*\|_\infty \\ \leq\gamma\|Q^{*,H-1}-Q^*\|_\infty \\ \leq \gamma^H\|Q^{*,0}-Q^*\|_\infty\\ \leq \gamma^H\frac{R_{max}}{1-\gamma}\)
Another prove: \(V^{\pi,H}(s):=\mathbb{E}[\sum_{t=1}^H\gamma^{t-1}r_t|\pi,s_1=s]\)
\[V^{*,H}=\max_\pi V^{\pi,H}(s)\] \[Q^{*}-Q^{*,H}\leq Q^*-Q^{\pi^*,H} \\ (since \ \pi^* is \ optimal \ for \ infinity \ horizon, but \ not \ when \ evaluated \ in \ H \ horizon)\\ =Q^{\pi^*}-Q^{\pi^*,H}\\\]For $\forall s,a, $ \(Q^{\pi^*}(s,a)-Q^{\pi^*,H}(s,a)=\mathbb{E}[\sum_{t=H+1}^\infty \gamma^{t-1} r_t|s_1=s,a_1=a,\pi^*]\\ \leq \gamma^H(\sum_{t=1}^\infty \gamma^{t-1}R_{max})\\ =\gamma^H\frac{R_{max}}{1-\gamma}\)
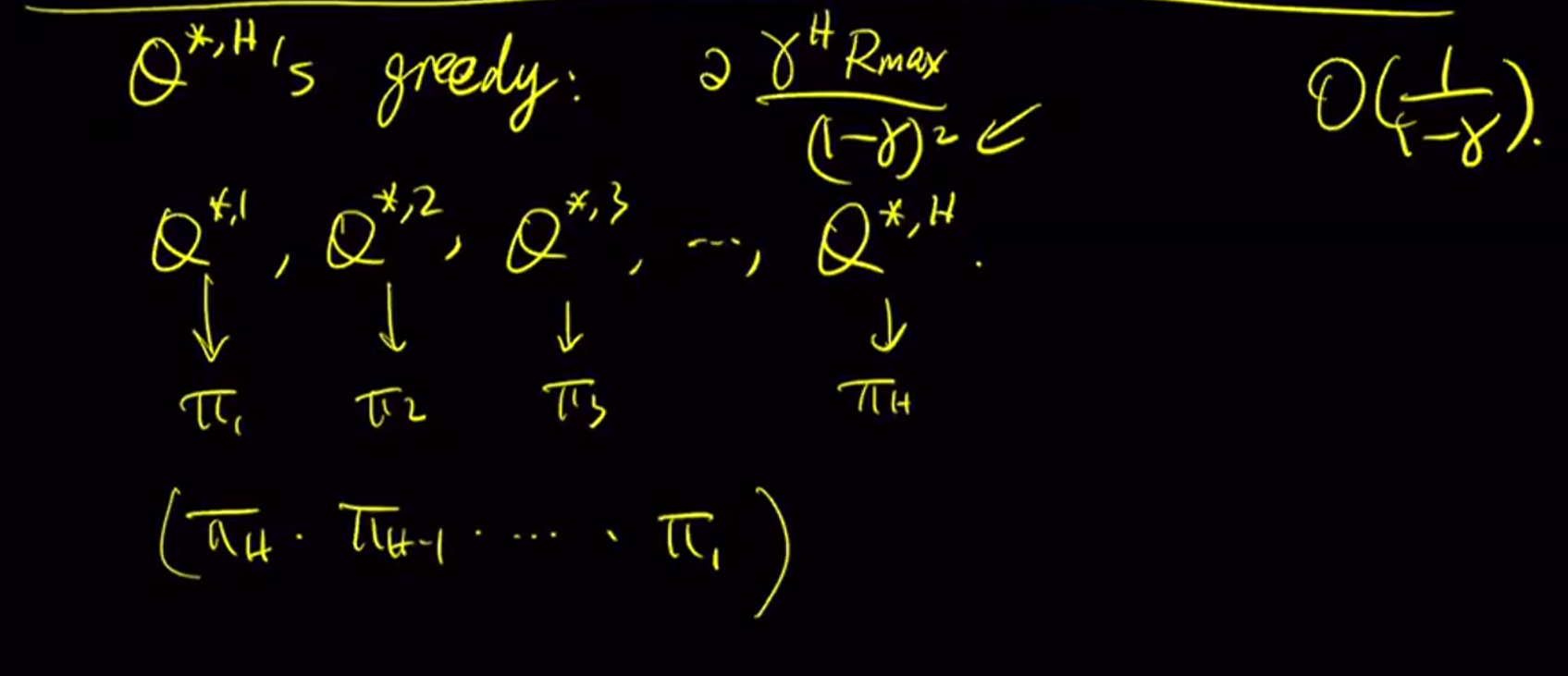
If we use a non-stationary policy that we execute $\pi_i$ in the i-th step, then the bound can be reduced from $O(1/(1-\gamma)^2)$ down to $O(1/(1-\gamma))$.
exercise
